Image

Master of Science in Mathematics

PROGRAM DESCRIPTION

The Master of Science in Mathematics (MS Math) program of UP Baguio provides students with a firm grounding in theoretical mathematics to prepare them for doctoral studies, research, careers in industry and government, and for teaching junior and senior level undergraduate mathematics courses.

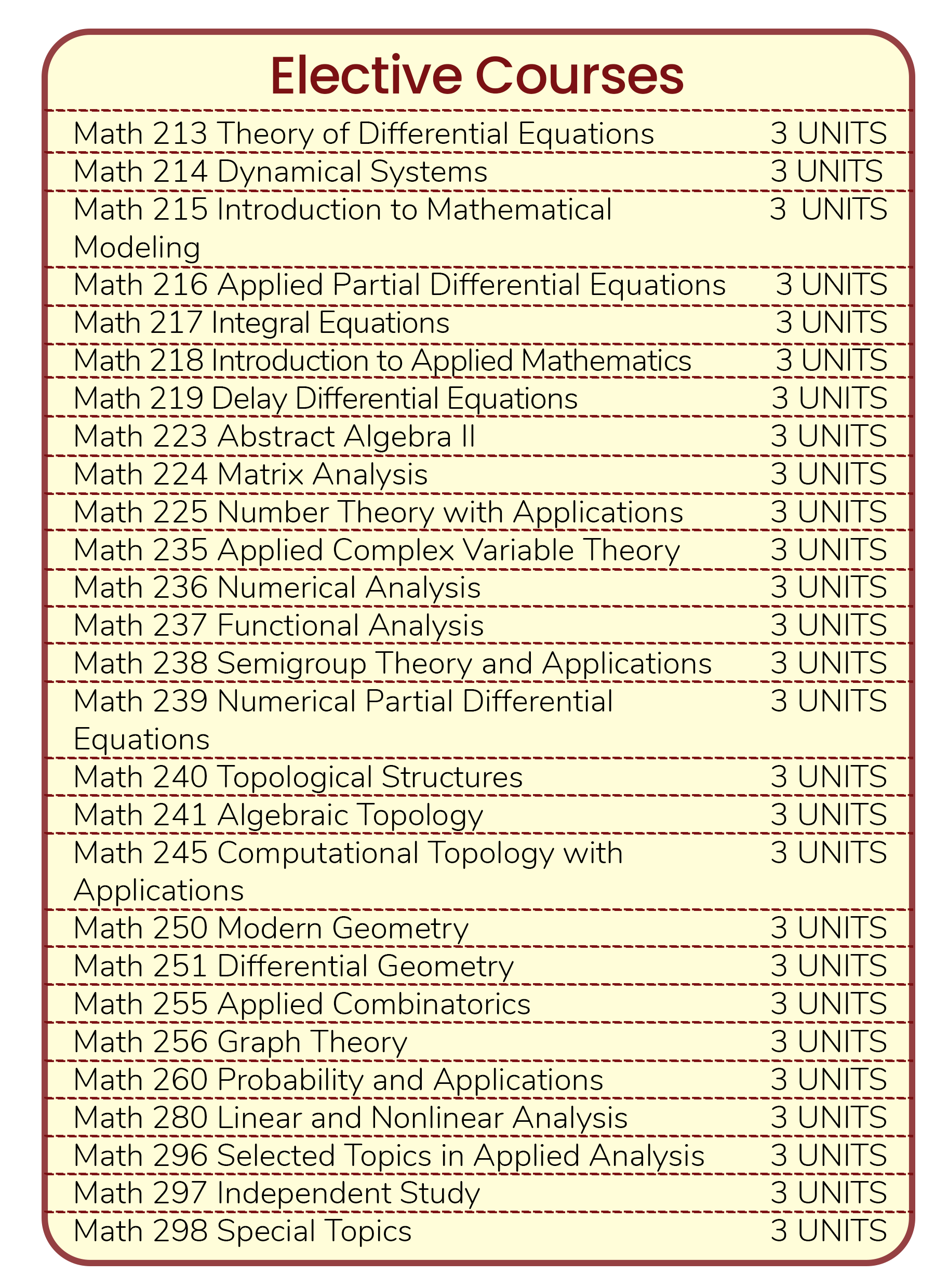
The MS Math curriculum is designed to allow the student an in-depth study of standard graduate courses in Analysis and Algebra, and electives that would lead the student to a specialization area of mathematics in preparation for his/her research work. The curriculum also helps the student in applying the mathematical tools to problems in other disciplines, such as Engineering, Physics, Life Sciences, Computing Sciences, Statistics, Finance and even the Social Sciences.


COURSE STRUCTURE

Non-Thesis Option

A student is required to take 33 units of graduate courses, pass a comprehensive examination in two (2) parts (Algebra and Analysis), and do an oral paper presentation on an area chosen by the student in consultation with at least one Mathematics faculty.

Courses
Units
Required
 12
Electives
 21
Total
 33

A student is eligible to take the comprehensive examination upon completion of 33 units of graduate courses, with a general weighted average of 2.00 or better.

Thesis Option

A student is required to take 30 units of graduate courses, and submit and a Master’s thesis for defense.

Courses
Units
Required
 12
Electives
 12
Thesis
 6
Total
 30

A student is required to make a satisfactory oral presentation of the master’s thesis, obtain a rating of ‘Passed’ from the Master’s thesis examination panel, and submit to the college 6 bound and certified copies of the approved Master’s thesis.

Required Courses

Course Number
Course Title
Units
Math 221
 Abstract Algebra
3
Math 222
 Linear Algebra I 3
Math 232
 Real Analysis
3
Math 234
 Complex Analysis 3
     

Electives

Courses
Units
Math 213 Theory of Differential Equations
 3
Math 214 Dynamical Systems
 3
Math 215 Introduction to Mathematical Modeling
 3
Math 216 Applied Partial Differential Equations
 3
Math 217 Integral Equations
 3
Math 218 Introduction to Applied Mathematics
 3
Math 219 Delay Differential Equations
 3
Math 223 Abstract Algebra II
 3
Math 224 Matrix Analysis
 3
Math 225 Number Theory with Applications
 3
Math 235 Applied Complex Variable Theory
 3
Math 236 Numerical Analysis
 3
Math 237 Functional Analysis
 3
Math 238 Semigroup Theory and Applications
 3
Math 239 Numerical Partial Differential Equations
 3
Math 240 Topological Structures
 3
Math 241 Algebraic Topology
 3
Math 245 Computational Topology with Applications
 3
Math 250 Modern Geometry
 3
Math 251 Differential Geometry
 3
Math 255 Applied Combinatorics
 3
Math 256 Graph Theory
 3
Math 260 Probability and Applications
 3
Math 280 Linear and Nonlinear Optimization
 3
Math 296 Selected Topics in Applied Analysis
 3
Math 297 Independent Study
 3
Math 298 Special Topics
 3

ADMISSION PROCESS

Applicants for admission to the MS in Mathematics program are expected to have completed a Bachelor’s degree in Mathematics, Computer Science, Statistics, Engineering or its equivalent from a recognized institution of higher learning. A prospective student is expected to have taken Differential and Integral Calculus, a course in Linear Algebra, Introduction to Differential Equations, and an Introduction to Probability and Statistics. Students should also have a knowledge of any of the following programming languages: Matlab, Scilab, Pascal, C, Fortran, or Java. A student with some deficiencies in these admission requirements may be admitted to the program on the condition that the corresponding undergraduate course is taken.

Documents to be Submitted for Admission:

  • Application Form for admission to a graduate program (UPB-GP Form No. 1, available at http://gpo.upb.edu.ph/forms-fees 
  • Transcript of Records undergraduate and graduate work, original and two (2) photocopies. (Validity of OTR will be determined from the remarks indicated thereof.) 
  • Three Reference - Report Forms from the applicant’s immediate supervisor (1) and former professors (2)
  • Recent 2” x 2” Photo (4 copies)
  • For working students: an official permit from his/her employer/supervisor indicating the maximum number of units the students is allowed to enroll.
  • For married women: 2 Photocopies of Marriage Certificate
  • For foreign students (non-English): passing the Test of English as a Foreign Language (TOEFL). A TOEFL score of 500 is required of an applicant whose medium of instruction in school/s attended is not English.
  • Birth Certificate (2 photocopies)

FACULTY PROFILE

Addawe, Joel M.
Ph.D. Mathematics
University of the Philippines, 2012

Addawe, Rizavel C.
Ph.D. Statistics 
University of the Philippines, 2018

Alangui, Wilfredo V.
Ph.D. Mathematics Education
University of Auckland, 2010

Bacani, Jerico B.
Dr.rer.nat. Mathematik
Karl-Franzens-Universitaet Graz, 2013
Collera, Juancho A.
Ph.D. Mathematics
Queen's University, 2012

Gueco, Edna N.
Ph.D. Mathematics
University of the Philippines, 2012

Ignacio, Paul Samuel P.
Ph.D. Mathematics
University of Iowa, 2019

Macansantos, Priscilla S.
Ph.D. Mathematics
University of Delaware, 1996
Manongsong, Saraleen Mae M.
Ph.D. Mathematics
University of the Philippines, 2020

Peralta, Gilbert R.
Dr.rer.nat. Mathematik
Karl-Franzens-Universitaet Graz, 2014

CONTACT INFORMATION

 DMCS Graduate Program Coordinator

University of the Philippines Baguio
Gov. Pack Road, Baguio City 2600
Tel. No, +63 (074) 442-7231
Fax No. +63 (074) 444-3128
 

Download Application forms at http://gpo.upb.edu.ph/forms-fees

 
Submit applications to:
The Graduate Program Office
University of the Philippines Baguio
Gov. Pack Road, Baguio City 2600
  Telefax No. +63 (074) 442-2460
E-mail: gpo.upbaguio@up.edu.ph

Main Menu